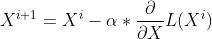The Backbone of AI

Gradient Descent

Welcome! I’m excited to release my first substack as I truly believe anybody is capable of getting into AI.

I released a poll on my twitter a while back to collect some topics that you all may be interested in. I hope to cover each of these topics over time but if there’s anything you’d like to see in particular please let me know in the comments.

Why Study AI?

With AI growing exponentially within the last decade there’s no better time to get into AI. If you follow the space at all, you’ve definitely heard of some of the more popular use-cases such as:

• AlphaFold, which generates 3D models of proteins

• AlphaGo, the first computer program to defeat a professional human Go player

• Github Copilot, an AI autocomplete for coding

• Tesla’s Autopilot and FSD

• Image Detection/Classification

Then there’s some of the more fun parts of AI such as generating faces of people that don’t exist (or this NSFW alternative), making an AI play Flappy Bird, etc.

Resources

Throughout the substack, I’ll cover enough for you to be able to start training/creating your own AI models; however, if you’re looking to get deep into the topic I suggest you look into the following resources:

• Calculus

• Linear Algebra

• Pattern Recognition and Machine Learning

• Introduction to Statistical Learning

• Neural Networks

• Deep Learning Book (This book also covers a bit of probability/statistics)

• NYU’s Deep Learning Course

The gatekeepers out there will try to tell you that you need to be a math expert to get into this field but that’s bullshit. If you’re going to get into research then you’ll absolutely need to deeply understand the math, but most people can get started by just watching those Calculus/Linear Algebra videos I linked above.

What is AI?

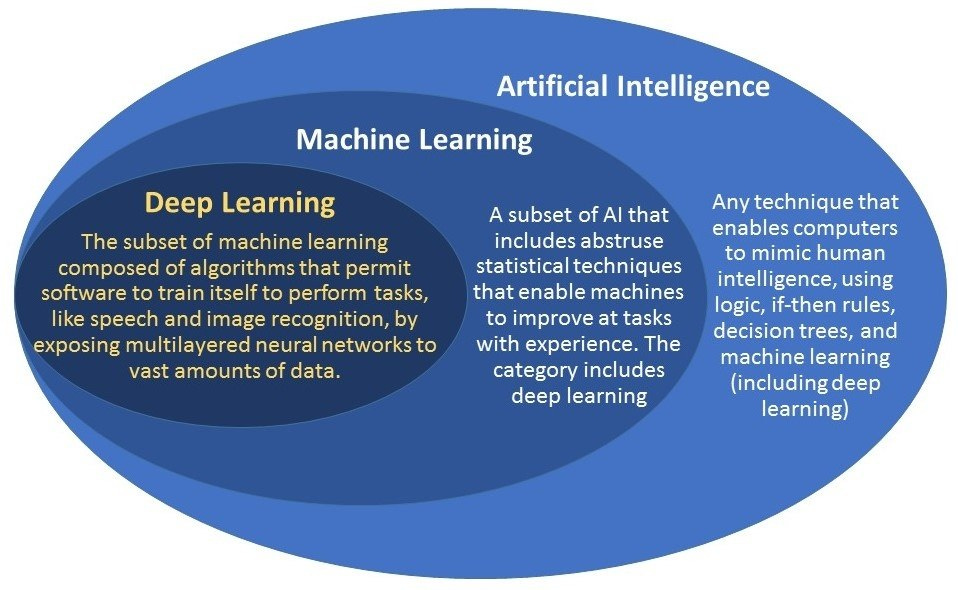
There’s a lot of confusion in the general public on what AI actually is. The term is used loosely but the Venn diagram below provides a more specific definition as well as the subsets that AI encompasses.

We’ll mainly be focusing on Deep Learning which was built upon numerical optimization methods. If you don’t know what that means don’t stress, the most important concept we’ll need to understand is Gradient Descent. Before we get into that, you’ll need to understand what a Neural Network is.

Neural Networks

I’ll briefly cover what a vanilla neural network looks like but I highly recommend watching the Neural Networks video I linked above. 3Brown1Blue does a tremendous job of explaining these topics and the videos are a great visual aid.

Let’s say we want to provide our computer an image and have it transform that into a label. For example, we’ll use BowTiedBull’s logo:

To do so, we can make a neural network like the one below.

This is a simple artificial neural network consisting of one hidden layer. Another term for this type of network is Multilayered Perceptron (MLP) or feedforward network. Feedforward just means that the information is flowing in one direction. This network would simply be:

where:

• x is a vector representing our input - BowTiedBull’s logo flattened into a vector of pixel values

• W are the weights of the Hidden Layer

• b are the biases of the Hidden Layer

• f(x) would be our output - the “BowTiedBull” label.

Prior to the output there’s usually an Activation Layer, I’ll cover this in a later post.

The weights and biases are the learnable parameters of this network. In order for a network to learn, we need to define a loss function (also called a cost function). We’ll go over some common loss functions in the future. For now, you can think of it as some function that distinguishes the error between our predicted output and expected output. Our goal is to minimize the amount of error we see from our predictions and we can do so by manipulating the weights/biases using Gradient Descent.

Gradient Descent

There are many different ways to find the minimum of a function but the method used in Deep Learning is Gradient Descent. If you’re unfamiliar with Calculus, I advise you brush up on how a derivative/gradient is calculated.

A gradient is essentially the steepest slope of ascent at a given point. To get to the minimum of our loss function, we’ll need to take step in the opposite direction. To understand how this work intuitively, you can imagine yourself stuck at the top of a mountain where you can only see a couple of feet around you due to some fog. If your goal is to get to the bottom of the mountain as quickly as possible, you’d look around to find the steepest step downwards and head in that direction. As you continue to do this, you’ll find yourself closer and closer to the bottom of the mountain. This is not an original example but I personally find it to be the most intuitive way of understanding gradient descent.

To illustrate this we’ll use a simple parabola as an example cost function. Head over to this python notebook on Google Colab to follow along.

First we import some libraries, Numpy and Matplotlib. We define our parabola function and the derivative of that function. Then some inputs and outputs are generated so we can view what our error surface would look like.

import numpy as np
import matplotlib as plt

# define a simple cost function for visualization, here we're using a parabola
def cost_function(x):
    return (x-1) ** 2

# define the gradient of our cost function
def cost_gradient(x):
    return  2*x-2

# generate some inputs to our function
inputs = np.linspace(-3,5,81)

# get the outputs of our cost function
outputs = cost_function(inputs)

# plot it
plt.plot(inputs,outputs)
plt.xlabel('Parameter value')
plt.ylabel('Cost function')
plt.title('Error Surface')

Next, we define a function that performs gradient descent on this function with tunable parameters.

from ipywidgets import interactive

# define function to perform gradient descent 
def descend(numIterations, learningRate, startingPoint):
    
    # array for storing our inputs
    xPath = np.empty(numIterations,)
    xPath[0] = startingPoint
    
    # perform gradient descent
    for iteration in range (1, numIterations):
        derivative = cost_gradient(xPath[iteration - 1])
        xPath[iteration] = xPath[iteration - 1] - learningRate * derivative
    
    # plot our error surface and results
    plt.plot(inputs,outputs)
    plt.plot(xPath, cost_function(xPath),'-o')

interactive_plot = interactive(descend, numIterations=(1, 20), learningRate=(0.1, 1), startingPoint=(-2, 5))

Under the comment # perform gradient descent we see the iterative process of taking a step in the opposite direction of the gradient. We evaluate the derivative of our cost function at the given input and store it in the variable derivative. We can then adjust our input using this value by subtracting it from our current input multiplied by the learningRate parameter. Mathematically, this looks like:

where X is our input, i is the current iteration, α is the learning rate, and L(X) is our loss function.

I’ve made it so you can modify the number of iterations, learning rate, and the initial starting point. We haven’t covered the learning rate yet but for now all you need to know is that it is a value that adjusts the size of the step you’re going to take. If you’re using the notebook I provided, try messing with these values in the interactive tool.

With numIterations=10, learningRate=0.7, and startingPoint=4 we get the results above. You can see with each iteration we get closer and closer to the minimum.

What To Expect

In the next post we’ll build upon what I covered by building and training a small network. I’ll go over some of the popular libraries, what I use most frequently and why, etc. Over time we’ll dive into some object classification and object detection models using Convolutional Neural Networks. My expertise is mostly in Computer Vision but if there’s anything you’re specifically looking for you can mention it in the comments!

Shoutout to BowTiedHAL for proof-reading and advice on content. Follow him on twitter if you don’t already.